2021-11-05

相続税対策となる永久国債

国債税制

　最近、日銀保有国債を永久国債化するという提案をしている政党がありますが*1, *2、あまりにも無責任です。

　中央銀行に多額の国債を買わせてはいけません。既に日本では、日銀の多額の国債保有によって、インフレ時に金融引き締めする方法がなくなっています。金融引締めを行うためには、日銀当座預金に付利して、金利を引き上げれば、日銀はすぐに債務超過に陥ります。

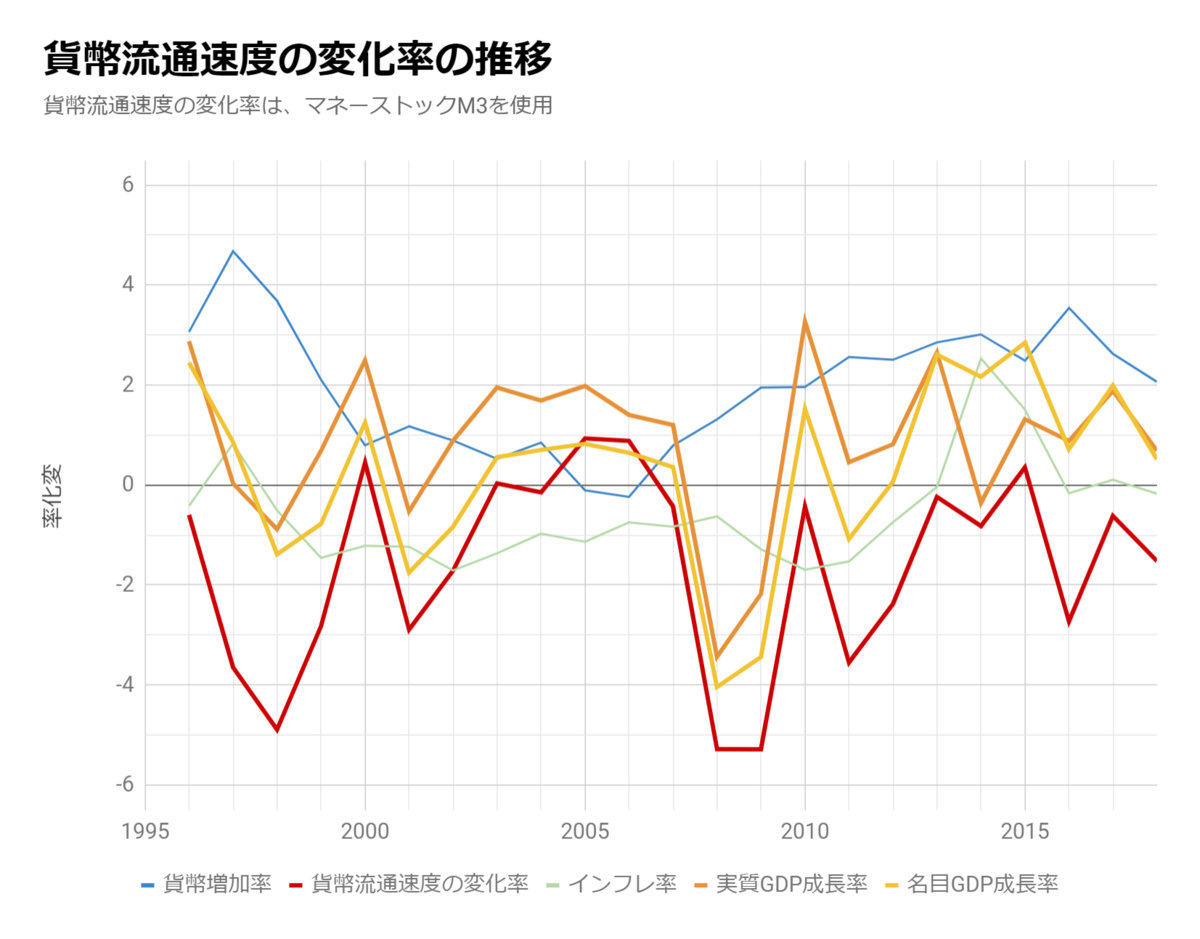
　中央銀行や民間銀行が、国債を購入すると、マネーストックが増加しますが、そのマネーストックが多額になることを避けるために、戦時中でも、国民に国債を推奨していました。いまは、マネーストックを増やしても、ほとんどがタンス預金化するので、インフレになりませんが、いざ、インフレになったときには収拾が付かなくなるでしょう。

　そこで、本稿では、国民に購入してもらえるような永久国債について考えました。相続税対策となる永久国債です。

f:id:toranosuke_blog:20211105185053j:plain:w500

1. 節税対策としての永久国債

　償還されない無利子の国債はゴミです。資産価値はありません。有利子であれば、少しは価値がありますが、非常に低金利であるならば、資産価値としては低いですが、一応は保有価値はります。

　低金利でも購入する魅力がある永久国債について提案します。ズバリ節税対策のための国債です。

　この永久国債は、次のメリットがあります。

　① 永久国債は、相続税の課税対象から除外する。
　② 永久国債は、相続税の納税のために物納できる(但し、上限あり)。

2. 相続税の課税対象から除外

　例えば、全財産を永久国債にすれば、課税対象額はゼロ。納税することなく、すべての財産を次世代に引き継ぐことができます。でも、現金化できるわけでもないので、わずかばかりの利子を貰うだけでは、保有資産としては魅力ありません。税金を支払ってでも、普通の資産を残した方が良いでしょう。

　とはいえ、100億円で金利年1%の永久国債、毎年1億円の金利が得られるなら、間違って魅力的に感じる人もいるかもしれません。100億円を貰うためには100年かかるのですけどね。少なくとも、子供の世代では元本相当額は使えない。その間にインフレがあれば、元本の実質価値も減っていく。そこのところを誤魔化すために、永久国債ではなく「償還期限の定めのない国債」にすると、いつかは償還されるのかなと、誤解する人も増えるでしょう。ほとんど国家詐欺ですが(笑)。

3. 物納を可能にする

　では、相続税の納税のために物納できたら、どうでしょうか？

　例えば、全財産100億円として、税率50%、全財産の1/3の永久国債を購入したとします。

課税対象額は、全財産の2/3 (66億円)
納税額は、課税対象額の50%の1/3 (33億円)
納税後財産は、全資産の2/3（67億円)

つまり、

節税対策なし：納税額50億円、納税後財産50億円
節税対策あり：納税額33億円、納税後財産67億円

　実に17億円も納税額を少なくすることができます。

　さすがに、これは財務省が許さないです。

　物納で永久国債が魅力的になるのは、永久国債が現金化(償還)されることと等価だからです。つまり、永久国債でなくなる抜け道を作っていることになります。

4. 物納額に上限を付ける

4.1 物納上限値

　物納可能にすると、あまりにも魅力的な金融商品になりすぎるので、物納に上限を設けることとします。

　全財産を x、国債保有比率を y、税率を z とすると、

節税対策しない場合、納税後資産は、x-xz = x(1-z)
節税対策する場合
- 保有国債残高は、xy
- 納税額は、x(1-y)z
- 納税後資産は、x-x(1-y)z = x(1-z)+xyz

　つまり、節税額は xyz となります。この節税分は永久国債となるように、物納額の上限を設けるとします。物納した後でも、節税額以上の国債保有することを条件とすると、物納額 a は、次の条件式を満たす必要があります。

　xy-a ≥ xyz

　つまり、

　a ≤ xy(1-z)

　物納の上限値は a = xy(1-z) となります。

　a=xy(1-z) のとき、納税後保有国債と節税額が等しくなります。つまり、節税メリットは永久国債保有だけになります。

国債保有比率 y=1/3、税率 z=1/2 の場合

　例えば、先の事例は、国債保有比率 y=1/3、税率 z=1/2 ですが、このときは次のようになります。

物納上限額は、a=xy(1-z) = x(1/3)(1-1/2) = x/6 (17億円)
納税額は、xz(1-y) = x(1/2)(1-1/3)=x/3 (33億円)
- 納税内訳は、現金納税：x/6 (17億円)、国債物納：x/6 (17億円)
納税後資産は、現金等：x/2 (50億円)、国債：x/6 (17億円)

　つまり、納税後資産は、50億円の財産に加えて、17億円の国債が残ります。この17億円の国債が節税効果になります。

　17億円の国債といっても償還されない国債なので資産価値としては低いですが、節税対策しないよりはお得です。

　国債の金利にもよりますが、このぐらいの節税効果なら、財務省も了承するでしょう。

4.2 最適な国債保有比率

　もっともお得な国債保有比率 y はどのようなものでしょうか？

　現金納税しない条件のもと、もっともお得な国債保有比率 y を求めたいと思います。

　物納上限値 xy(1-z) と納税額が xz(1-y) が等しくなる国債保有比率 y のときに、納税後の国債を含めた財産が最大となります。

　xy(1-z) = zx(1-y)

つまり、

　y=z

　税率と同じ割合だけ、国債を保有したときが、最もお得です。

　永久国債の金利を考慮すると、最適値は変わります。いろいろと面倒なので略。

y=z=1/2の場合

物納上限額は、a=xy(1-z)=x(1/2)(1-1/2)=x/4 (25億円)
納税額は、xz(1-y) = x(1/2)(1-1/2)=x/4 (25億円)
- 納税内訳は、国債物納：x/4 (25億円)、現金納税：0
納税後資産は、現金等：x/2 (50億円)、国債：x/4(25億円)

　節税対策によって、25億円の国債が財産として加わります。

4.3 物納上限を言葉で表す

　a < xy(1-z) の条件を言葉で表すと、例えば、次のようになります。

　「保有国債残高に税率をかけた額(xyz)を保有国債残高(xy)から減じた額(xy-xyz)を上限に物納を可能とする」

　何を言っているか分からない(笑)。税理士に相談しましょう。

5. 増税

　さて、これだけだと、国からすれば、税収変わらずで、永久国債の負債を抱えただけになります。

例えば、y=z=1/2の場合

節税対策なし：収入50億円
節税対策あり：収入50億円、国の負債(永久国債)：25億円

　このため、国の収入を増やすためには増税をセットで導入する必要があります。

5.1 税率を50%から75%にあげた場合

　例えば、x=100億円、y=z=3/4 (相続税率75%)の場合、

節税対策なし
- 国側　：収入75億円 (内訳：相続税75億円)、負債：0
- 相続側：支出75億円 (内訳：相続税75億円)、納税後資産：現金等25億円
節税対策あり：
- 国側　：収入75億円 (内訳：国債売却75億円)、負債：国債18.75億円
- 相続側：支出75億円 (内訳：国債購入75億円)、納税後資産：現金等25億円＋国債18.75億円＝43.75億円)
  - 国債購入：xy=3x/4 (75億円)
  - 物納上限=x(3/4)*(1-3/4)=3x/16 (18.75億円)
  - 納税額=x(3/4)(1-3/4)=3x/16 (18.75億円)
    - 納税内訳：国債現物3x/16 (18.75億円)、現金納税0
  - 納税後資産は、現金等：x/4 (25億円)、国債：3x/16 (18.75億円)、計7x/16 (43.75億円) *増税なし(y=1/2)、節税なし：
- 国側：収入50億円
- 相続側：納税50億円、納税後資産50億円

　この場合、相続税率 50% から 75% への増税により、国の収入は25億円増、負債は18.75億円増となり、相続側は、納税後資産は50億円から43.75億円への6.25億円減少に留まります。

5.2 納税後も「資産」が減らない国債保有比率

　増税前の納税後資産と、増税後の納税後の国債を含めた資産が、同じとなる国債保有比率を求めることにします。

増税前の税率の税率を z、増税後の税率を z'、増税後の国債保有比率を y' とします。納税後資産は次のようになります。

　増税前の節税対策がない場合の納税後資産：x(1-z)
　増税後の節税対策がある場合の納税後資産：x(1-z')+xy'z'

　これからが等しくなる国債保有比率 y' を求めると、

　相続税の税率を50%から100%にしたときに、納税後資産が変わらないように国債購入をしたときのシミュレーションを図に示します。

f:id:toranosuke_blog:20211106185033p:plain

f:id:toranosuke_blog:20211106185222p:plain

6. 最後に

　多少の金利がついても永久国債などは全く魅力のない金融商品ですが、節税対策になる税制を付け加えることで、魅力的な金融商品に変貌します。

　既に米国では、テーパリングが議論されていますが、いまのままでは日本は国債の買い手がなく無理でしょう。国の資金調達のために日銀は国債を買い続けることになります。

　このような事態を避けるために、節税対策となる国債などを発行して、国債の買い手を開拓する努力をすることが、国には求められるのではないでしょうか？

　なお、永久国債を日銀に買わせろというのは論外ですが、節税対策国債の発行で買い手ができるから、さらに国債を発行しようというのも論外です。悪しからず。

(2021/11/5)

*1:ロイター「日銀保有国債の一部永久国債化による財源確保、慎重に検討必要＝岸田首相」(2021.10.13).

*2:国民民主党政策パンフレット (2021).

2019-09-14

ドーマーの定理の証明（６）：貨幣数量説に基づく国債残高の収束性

ドーマーの定理貨幣数量説フィッシャーの交換方程式貨幣回転率預金課税

f:id:toranosuke_blog:20190911151607j:plain:w500

　ドーマーの定理の一連の記事を書くきっかけは、「インフレ率が上がるまでは、国債発行しても構わない」という反緊縮派の主張にあります。もしかしたら、このインフレ制約があると、ドーマーの定理の条件を満たすのではないかという疑問があり、記事を書き始めました。今回の記事がその疑問への回答になります。

　結論は、条件によってはドーマーの定理を満たすが、条件によってはドーマーの定理を満たさず財政破綻する（対GDP比の国債残高は発散する）、です。

　その条件とは貨幣流通速度です。

　貨幣流通速度が一定、あるいは、上昇していれば、ドーマー条件を満たして、国債残高の対GDP比は収束します。これは当初の予想通りでした。

　しかし、貨幣流通速度が低下していけば、ドーマー条件を満たさず、国債残高の対GDP比は発散します。

　このため、貨幣流通速度の低下を食い止めることが、国債残高の対GDP比が発散しないために、非常に重要となります。

　さて、前回の記事では、インフレ率がゼロのもとでの国債発行額（＝貨幣発行量）を貨幣数量説に基づいて示しましたが、今回の記事は、貨幣数量説からの考察をインフレ率だけではなく、より一般化して、インフレ率・GDP成長率・貨幣流通速度を含めて考慮したうえで、国債発行額と国債残高の収束性について検討したいと思います。

1. 貨幣数量説に基づく国債残高の収束性

　今回、証明するのは、次の命題です。

貨幣数量説に基づく国債発行額と国債残高の収束性

　① インフレ率 $p_t$ が特定の値となるように毎年の国債発行額 $b_t$ を決める場合、国債発行額と実質GDP成長率 $y_t$ 、貨幣流通速度の変化率 $v_t$ と貨幣量 $M_t$ の間には、次の関係が成り立つ。

$\displaystyle \begin{eqnarray} ~~~~b_t & = & (p_t + y_t - v_t )~ M_t \end{eqnarray}$

　② 名目GDPがプラス成長で、貨幣流通速度が上昇、もしくは、安定していれば、国債残高の対GDP比は収束する。

　③ 名目GDPがプラス成長でも、貨幣流通速度が低下していれば、国債発行額の対GDP比は増大していき、国債残高の対GDP比は発散する。

(但し、民間貸出に伴う貨幣供給は、無視できる場合)

　３つ目の命題は、別の言い方をすると、国債発行して、貨幣量を増やしても、その端からお金を溜め込んでいかれては、たとえ、経済成長していても、政府債務はどんどんと増えていって、財政破綻するということです。

　日本の貨幣流通速度は低下し続けていますが、貨幣流通速度を上げていかないことには、対GDP比の国債残高を減らすことができないことをこの命題は示しています。

2. 証明

2.1 フィッシャーの交換方程式

　貨幣数量説におけるフィッシャーの交換方程式によれば、貨幣増加量 $m_t$ 、貨幣流通速度の変化率 $v_t$ 、インフレ率 $p_t$ 、実質GDP成長率 $y_t$ の間には、次の関係があります。

　この関係は、通常用いるフィッシャーの交換方程式を微分することで導くことができます*1。また、右辺の $p_t+y_t$ は、名目GDP成長率 $g_t$ を表しています。

2.2 国債発行額

　インフレ率が $p_t$ となるように（あるいは、名目GDPが $g_t$ となるように）、国債を発行する場合を考えます。（民間貸出に伴う貨幣供給が無視できれば）このときの発行すべき国債額 $b_t$ は、必要な貨幣増加量 $\Delta M_t$ と等しくなりますので、

　従って、インフレ率を $p_t$ とするために必要な国債発行量 $b_t$ は、フィッシャーの交換方程式から次式となります。

　実際には、財政支出によって、 $p_t$ 、 $y_t$ 、 $v_t$ は影響を受けるので、過去の実績から予測して、目標のインフレ率 $p_t$ となるように国債発行額　 $b_t$ を決めるか、あるいは、目標のインフレ率になるように漸近的に国債発行額を増加させることになると思います。

　ここでは、民間貸出に伴う市中銀行による貨幣供給は考慮に入れていませんが、民間貸出を考慮した場合については、付録で検討しました。

2.3 国債発行額の対GDP比

　次に国債発行額 $b_t$ の名目GDP $G_t$ に対する比率 $\alpha_t$ を考えていきましょう。

　名目GDP $G_t$ は、名目GDP成長率 $g_t$ を用いると、次のように表すことができます。

　従って、国債発行額の対GDP比 $\alpha_t$ は、次式となります。

　ここで、 $m_t=p_t+y_t-v_t = g_t - v_t$ 　を代入し、

2.4 貨幣流通速度に対する収束性

貨幣流通速度が一定の場合、国債残高は収束する

　貨幣流通速度が一定の場合、国債残高の対GDP比は、ゼロ成長・プラス成長であれば、収束します。マイナス成長でも、国債残高が発散することはありません。

国債残高の対GDP比

　貨幣流通速度が一定、つまり、 $v_t$ =0 の場合について考えると、

　名目GDP成長率が一定でゼロでなければ、以前の記事の国債残高の対GDP比の式より、次式が得られます。

プラス成長の場合

　名目GDP成長率が、プラス成長（ $g$ > 0）であれば、第2項がゼロに収束し、国債残高の対GDP比は $\frac{M_0}{G_0}$ に収束します。

マイナス成長の場合

　名目GDP成長率が、マイナス成長（ $g$ < 0）であれば、次のようになります。

　マイナス成長の場合、国債発行額 $b_t$ (= $gM_t$ ) は負の値になりますが、国債を発行するのではなく、税によって貨幣を市場から吸い上げることを意味します。国債残高は縮小していきます。

　また、貨幣量が国債残高よりも小さいということはないので、 $B_0$ > $M_0$ となることはそもそもありませんので、無限大への発散はありません。

　 $B_0$ < $M_0$ の場合、ある程度時間が進行すると、国債残高 $B_t$ がマイナス残高、つまり、国がお金を貯める状況になります。

ゼロ成長の場合

　ゼロ成長 ( $g=0$ ) であれば、国債発行額 $b_t$ (= $gM_t$ ) もゼロで国債残高は増加せず、名目GDPも成長しないので、国債残高の対GDP比は変化せず、 $\frac{M_0}{G_0}$ のままです。

貨幣流通速度が上昇すれば、債務残高はゼロに収束する

　貨幣流通速度が上昇していく、つまり、貨幣流通速度の変化率 $v_t$ が正の場合を考えます。

　このとき、 $\displaystyle \frac{1+g_i-v_i}{1+g_i}\lt1$ ですので、

　従って、

　また、プラス成長であれば、ドーマーの定理により、国債残高の対GDP比はゼロに収束します。

　これは、貨幣流通速度が上昇することによって、たとえ、少ない貨幣量であっても、お金が何回も循環していくことで、所望するインフレ率が得られるということを意味します。

　実際には、貨幣流通速度には上限があると考えられるので、途中で $v_t$ =0となり、貨幣流通速度が一定の場合と同様に、ある国債残高に収束していくと考えられます。

貨幣流通速度が下降すれば、債務残高は発散する

　貨幣流通速度が下降していく、つまり、貨幣流通速度の変化率 $v_t$ が負の場合を考えます。

　このとき、 $\displaystyle \frac{1+g_i-v_i}{1+g_i}\gt 1$ ですので、

　プラス成長であれば、 $g_t-v_t$ ＞0となりますので、国債発行額の対GDP比率は発散します。

　国債発行額の対GDP比率が発散していくのであれば、国債残高も発散します。

　実際には、貨幣流通速度がどこまでも下降することはなく、貨幣流通速度が一定となり、国債残高の対GDP比は収束すると思いますが、それまでの間、貨幣流通速度の低下によって債務残高は増大していきます。

3. 具体例

3.1 簡単な例

　次の事例で国債発行額 $b_t$ を計算してみます。

インフレ率： $p_t$ = 1%
実質GDP成長率： $y_t$ =1%
名目GDP： $G_t$ = 500兆円
貨幣量： $M_t$ = 1300兆円（マネーストックM3）

貨幣流通速度の変化率 $v_t$ =0% の場合

貨幣流通速度の変化率 $v_t$ =-1.5% の場合

　最近のマネーストック統計M3の貨幣流通速度の変化率は、-1.5%程度です。この値を使って試算します。

　貨幣流通速度の変化率が0%から-1.5%に低下すると、国債発行額を約20兆円も増加させる必要があります。

3.2 2018年の日本のデータを用いた試算

　2018年のデータを用いて計算します。

名目GDP成長率 $g_t$ =0.51%（内閣府発表 *2）
　（実質GDP成長率 $y_t$ = 0.69%、インフレ率 $p_t$ =-0.17）
マネーストックM3 $M_t$ =1344兆円（2019年3月末、日銀発表 *3）
貨幣流通速度の変化率 $v_t$ = -1.52%（筆者推計 *4 ）

　2017年度(853.2兆円)から2018年度(880.2兆円)の普通国債残高の増加は27.0兆円*5、マネーストック統計M3の増加量は、2018年3月末(1316.9兆円)から2019年3月末(1344.1兆円)で27.2兆円です。若干のずれがあるものの、それぞれの数字は、一見、一致しているように見えます。

　しかし、市中銀行による貸出金の増加は、2017年3月末(493.7兆円)から2019年3月末(508.2兆円)の差で14.5兆円ありますので*6、それと普通国債残高の増加27.0兆円を合わせると、貨幣発行量は41.5兆円となり、マネーストック統計M3の27.2兆円の増加と大きく乖離しています。

　一般政府（国・地方自治体・社会保障基金）の債務を見ると、2017年度(1280.9兆円)から2018年度(1301.8兆円)と20.9兆円の伸びに留まり*7、普通国債残高の増加27兆円よりも小さな値になっています。

　一般政府債務と銀行貸出金の間には重複があると思われますが、まずは、マネーストック統計と貨幣発行量の統計値が一致しないことには、本稿の理論式の検証は難しいという印象です。

4. 貨幣流通速度低下時に債務が発散しない条件

　現在の日本の貨幣流通速度は低下を続けています*8。

　貨幣流通速度の変化率 $v_t$ が負の場合でも、実質GDP成長率 $y_t$ がプラス成長のもと、債務が発散しない条件について考えます。

　貨幣流通速度が低下する場合であっても、債務が発散しないためには、 $\displaystyle\frac{b_t}{G_t}$ の $(g_t-v_t)$ の項を負にして、 $\displaystyle\frac{b_t}{G_t}$ をゼロ以下にすることが必要です。つまり、国債発行をせず、財政黒字にする必要があります。

　つまり、貨幣流通速度が負である場合には、インフレ率の目標はマイナス、デフレとなるように貨幣供給することが必要です。また、このときの名目GDP成長率はマイナスです（ $g_t$ ≤ $v_t$ < 0 ）。

　なお、デフレであっても、 $y_t$ >0 となる条件はありますので、経済成長は可能です。

　財政黒字の条件から実質GDP成長率 $y_t$ の条件を導くと、

　右辺が正であれば、 $y_t\gt 0$ となり得ます。

　 $v_t$ 、 $p_t$ ともに負ですので、この式は、貨幣流通速度が低下スピードよりもデフレ率が大きければ、実質GDP成長するとことを表しています。

　貨幣流通速度の低下を条件とした場合に、実質GDP成長がプラス成長のもとで、債務残高を発散させないためには、①財政黒字を確保する、②デフレである、③貨幣流通速度の低下率よりもインフレ率の下げ率の方が大きいことが必要です。

　これは非常にハードルが高い条件のように思います。

5. 貨幣流通速度と成長率の関係

　1995年～2018年の日本の貨幣流通速度を以前調べましたが、およそ-5%～+1%の間で推移しています*9。また、名目GDP成長率はおよそ -4%～-+3%、実質GDP成長率はおよそ-3%～+3%で推移しています。

f:id:toranosuke_blog:20190911235037p:plain

　この推移を見ると、貨幣流通速度と実質GDP成長率・名目GDP成長率に相関があることが分かります。これは散布図にすると、良く分かると思います。

f:id:toranosuke_blog:20190911235728p:plain

　国債残高の対GDP比を発散させないためには、まず、貨幣流通速度の変化率を正の値にすることが肝要です。

　散布図を見ると、名目値でも、実質値でも、GDP成長率が1%を超えると、貨幣流通速度は-1%～+1%の間で分布するようになっています。

　このことから、GDP成長率がある程度高くなると、貨幣流通速度も上昇することが期待できます。但し、因果関係として、GDP成長が貨幣流通速度の向上をもたらすのか、貨幣流通速度の向上がGDP成長をもたらすのかは議論の余地があります。

6. 貨幣流通速度を上昇させるための税制

6.1 眠った現預金は貨幣流通速度を低下させる

　貨幣流通速度の低下は、人々が貯蓄を行って、あまりお金を使わなくなっていることを意味します。

　貯蓄の目的は、住宅購入・教育資金のための頭金や老後資産などの将来的な貯えかもしれませんし、将来の経済危機に備えた企業の貯えかもしれません。富裕層の使いきれないお金であったり、特段の目的なく貯蓄をすることもあるでしょう。

　貯蓄は重要ですが、タンスに眠っているだけで、使われない現金（紙幣・硬貨）であれば、これは経済にとっては存在しないも同然です（タンス預金の貨幣流通速度はゼロです）。

　銀行に預けられている預金も同様です。貯めているだけで消費されなければ、貨幣流通速度（貨幣回転率）の増加に寄与しません*10。

　但し、同じ貯蓄であっても、債権や株式に投資されたお金であれば、それは企業活動に使われますので、眠ったお金にはなりません。

6.2 税金でお金の流れを誘導する

　税金は、国の活動のために集められるということもありますが、お金の使い方の誘導もできます。

　例えば、環境税は、環境負荷の抑制を目的に導入される税金です。税金を課すことによって、例えば、高いガソリン税を課せば、ガソリンの消費が抑制されます。レジ袋に税金を課せば、レジ袋を使うのを控えるようになるでしょう。消費に税金を掛ければ、消費が抑制されます。

　同様に、貯蓄を抑制したいのであれば、貯蓄へ税金を課せばよいということになります。特に問題なのが、現預金の貯蓄です。

　現金への課税は、法人を除けば困難ですので、筆者として、預金税が良いと考えています。預金税から得られた税収増を相殺するように消費税を減税すれば、税収は一定でも、貯蓄を抑制し、消費を活性化することができるでしょう。

　なお、預金税については、別記事で考察しています*11。

　預金税は、澱んで滞留してしまったお金を救い上げて、経済の循環の中に戻すという見方もできるでしょう。

7. 最後に

　今回は、次の命題を証明しました。

貨幣数量説に基づく国債発行額と国債残高の収束性

　① インフレ率 $p_t$ が特定の値となるように毎年の国債発行額 $b_t$ を決める場合、国債発行額と実質GDP成長率 $y_t$ 、貨幣流通速度の変化率 $v_t$ と貨幣量 $M_t$ の間には、次の関係が成り立つ。

$\displaystyle \begin{eqnarray} ~~~~b_t & = & (p_t + y_t - v_t )~ M_t \end{eqnarray}$

　② 名目GDPがプラス成長で、貨幣流通速度が上昇、もしくは、安定していれば、国債残高の対GDP比は収束する。

　③ 名目GDPがプラス成長でも、貨幣流通速度が低下していれば、国債発行額の対GDP比は増大していき、国債残高の対GDP比は発散する。

　貨幣流通速度が低下するというのは、簡単に言えば、お金が貯蓄されて使われないということです。

　国債発行額・発行貨幣量をいくら増やしても、お金が貯蓄され使われなければ、なかなか経済は成長しません。また、債務残高はどんどんと膨れ上がるということになります。

　このため、貨幣流通速度を上昇させる、または、安定させることによって、債務を発散させないようにすることが必要です。貨幣流通速度が安定すれば、財政赤字があっても、国債残高が発散することはありません。

(2019/9/14)

付録：民間貸出による市中銀行の貨幣供給

　ここまでの議論では、民間への貸出に伴う市中銀行による貨幣供給は考慮に入れていません。

　ここでは、民間貸出による貨幣供給も考慮にいれ、検討します。

　まず、貨幣量 $M_t$ を国債由来の貨幣 $M_t^B$ と、民間貸出由来の貨幣 $M_t^C$ に分けます。

　このとき、毎年の国債発行額 $b_t$ は、次式となります。

　ここで、 $m_t$ 、 $m_t^C$ は、それぞれ貨幣全体の貨幣増加率と、民間貸出に伴う貨幣の貨幣増加率です。

　国債発行額の対GDP比は、

　上式の第1項は、これまでと同じですが、第2項が付くことによって、 $v_t$ が負であっても、発散しない可能性が出ててきます。例えば、 $m_t^C>g_t$ 、つまり、名目GDP成長率よりも民間貸出の貨幣増加率が大きくなれば、発散しない可能性があります。

　もっとも民間貸出が多くなるような状況は景気が活発であるのでしょうから、貨幣流通速度も上昇していって、第1項も小さくなっていく局面であるかもしれません。

*1:インフレ率・経済成長率と貨幣量の変化率との関係式（フィッシャーの交換方程式からの導出） - ゲゼルマネー経済学入門

*2:内閣府, 「国民経済計算（GDP統計）：2019年1-3月期2次速報値」.

*3:日本銀行, 「時系列統計データ検索サイトマネーストック」.

*4:日本における貨幣回転率とその変化率 - ゲゼルマネー経済学入門

*5:財務省, 「戦後の国債管理政策の推移」

*6:日本銀行, 「預金・貸出関連統計（預金・現金・貸出金）」.

*7:世界経済のネタ帳, 「日本の政府債務残高の推移」.

*8:日本における貨幣回転率とその変化率 - ゲゼルマネー経済学入門

*9:日本における貨幣回転率とその変化率 - ゲゼルマネー経済学入門

*10:貨幣外生説の立場であれば、銀行預金に貯えられた預金は貸出に回されると考えますが、貨幣内生説の立場であると貸出金は銀行による貨幣創造によって賄われるため、預金を必要とはしません。預金に対応する貸出金や債券などの資産から銀行は金利得て、預金にも利息を付けますが、基本的には消費に使われるわけではないので、貨幣流通速度の向上に寄与しないお金と考えることができます。

*11:非課税枠付き預金課税と消費減税を同時実施した場合の損益分岐点 - ゲゼルマネー経済学入門

2019-09-06

ドーマーの定理の証明（５）：インフレ率ゼロのときの成長率と国債発行額の関係

ドーマーの定理貨幣数量説フィッシャーの交換方程式

f:id:toranosuke_blog:20190906194834j:plain:w300

　今回は、インフレ率との関係を考えてみたいと思います。実は、これがMMTにおける財政スペースと密接に関係しているのではないかと思っているのです。でも、MMTについては詳しくはないので、間違っているかも。

　貨幣数量説に基づいて、インフレ率をゼロになるように国債を発行すると仮定すると、毎年の国債発行額と実質GDP成長率との関係が定まります。今回はこの関係について説明したいと思います。

1. インフレ率ゼロのときの成長率と国債発行額の関係

　今回、証明するのは、次の命題です。

インフレ率ゼロのときの成長率と国債発行額の関係
　インフレ率をゼロとするように毎年の国債発行額を決める場合、国債発行額は、GDP成長率と同じ比率で貨幣が増えた時の貨幣増加量に等しい。また、国債残高の対GDP比率は、当初の貨幣量の対GDP比率に収束する。

2. 証明

2.1 貨幣数量説

　貨幣数量説によれば、ある時点 $t$ での貨幣量 $M_t$ 、貨幣流通速度 $V_t$ 、GDPデフレータ $P_t$ 、実質GDP $Y_t$ の間には、次の関係式が成り立ちます。

2.2 貨幣量の増加

　ここで、時点 $t$ と時点 $t$ +1 での間のインフレ率はゼロ、つまり、 $P_t$ = $P_{t+1}$ (= $P$ ) を仮定します。貨幣流通速度についても、 $V_t$ = $V_{t+1}$ (= $V$ ) で一定と仮定します。

　このときの関係式は、次の通りです。

　従って、

　時点 $t$ と時点 $t$ +1での貨幣の増加 $\Delta M_t$ は、次の通りです。

　ここで、 $y_t$ は、実質GDP成長率です。

　つまり、貨幣数量説の等式が成り立つためには、成長率に応じて、貨幣量の増加が必要となります。

　また、貨幣量 $M_t$ は、次式となります。

2.3 GDPの増加

　　実質GDP $Y_t$ が成長率 $y_t$ で成長するとき、実質GDPは次式となります。

　また、名目GDP $G_t$ は、次式です。

　なお、名目GDP成長率 $g_t$ と実質GDP成長率 $y_t$ は、インフレ率ゼロのため等しくなります。

2.4 GDPと貨幣量の関係

　貨幣量 $M_t$ と名目GDP $G_t$ の比を求めると、

　従って、

2.5 国債発行額と貨幣の増加量

　インフレ率ゼロにするために必要な新規貨幣の発行を国債発行額 $b_t$ に伴う政府支出で行うと仮定します。

　ここで、国債は、市中銀行あるいは中央銀行が引き受け、通貨発行するとします。また、国債以外の市中銀行の信用創造による貨幣供給は、無視します。

　つまり、国債発行額は、GDP成長率と同じ比率で貨幣が増えた時の貨幣増加量に等しくなります。

　なお、このとき、国債発行額の対GDP比 $\alpha$ は、

2.6 ドーマーの定理の適用

　実質GDP成長率 $y_t$ (= $y$ ) が一定で正であれば、ドーマーの定理*1により、国債残高 $B_t$ の対GDP比は、収束します。その収束値は、次の通りです。

　つまり、初期の貨幣量と名目GDPの比に収束していくということです。

3. 具体例

　例えば、貨幣量 $M_t$ をマネーストックM3の1300兆円、名目GDP $G_t$ を500兆円、実質GDP成長率 $y_t$ を2%とすると、発行可能な国債額 $b_t$ は次の通りです。

　また、このときの国債残高の対GDP比の収束値は、次のようになります。

　年間26兆円の国債を発行しながらも、国債残高比率は一定に保てます。

4. MMTとの関係

　MMTには、財政スペースという考えがあるようです。この財政スペースは、貨幣数量説的に説明すれば、潜在的な生産量（生産能力） $Y_1$ と現在の生産量（生産能力） $Y_0$ のギャップ $\Delta Y (=Y_1-Y_0)$ ということではないかと思います。

　この生産量のギャップ $\Delta Y$ は、生産資源が活用されていないために生まれます。活用されていない生産資源の例が、失業者のような人的資源です。この人的資源を有効活用するように、政府支出（=貨幣供給= $\Delta M$ ）を行うことで、資源を活用します（失業をなくします）。

　これが、ざっくりとしたMMTの解釈ですが、MMTerの方には怒られるかもしれません。

　さて、貨幣数量説としては、貨幣供給 $\Delta M$ に見合った生産 $\Delta Y$ がなければインフレが起こります。職業保証プログラム(JGP) では、その辺りはどうなっているのかなとちょっと気になるところではあります。

5. 最後に

　今回は、次の命題を証明しました。

インフレ率ゼロのときの成長率と国債発行額の関係
　インフレ率をゼロとするように毎年の国債発行額を決める場合、国債発行額は、GDP成長率と同じ比率で貨幣が増えた時の貨幣増加量に等しい。また、国債残高の対GDP比率は、当初の貨幣量の対GDP比率に収束する。

　今回の証明では、インフレ率はゼロ、貨幣流通速度も一定と仮定していますが、次回は、インフレ率・貨幣流通速度の変化も考慮した検討を行いたいと思います。

(2019/9/6)

*1:ドーマーの定理の証明（１）：元祖ドーマーの定理 - ゲゼルマネー経済学入門

2019-09-02

ドーマーの定理の証明（４）：成長率と金利・国債残高の制約式

ドーマーの定理利子率

f:id:toranosuke_blog:20190904172210j:plain:w400

　オリジナルのドーマーの定理において、毎年の国債発行額の対GDP比率を一定にするように基礎的財政収支を決めるとすると、成長率と金利・国債残高の間には制約が生じます。

　今回は、この制約関係について説明します。

1. 成長率と金利・国債残高の制約関係

　ドーマーの定理の条件を満たすように、毎年の国債発行額の対GDP比率を一定にしたとき、GDPの成長に伴って国債発行額に余力が生まれます。一方、利払い費（＝国債残高×国債金利）が上昇すれば、国債発行額の余力を奪われます。この制約関係を金利が制御できるとして金利の制約条件として考えると、次の条件式が得られます。

成長率と金利・国債残高の制約式
　ドーマーの定理の条件を満たしながら、GDPが成長するとき、基礎的財政収支の赤字を大きくし、財政支出の余力を増やすためには、金利は次の条件を満たさなければならない。

$\displaystyle \begin{eqnarray} r_{t+1} & \le & \frac{\alpha g_t G_t + r_t B_t}{\alpha G_t+B_t} \\ ~~\\ ここで、\\ \alpha & ：& \mbox{国債発行額の対GDP比率（一定の値）}\\ g_t & ：& \mbox{名目GDP成長率}\\ r_t & ：& 国債金利\\ G_t &：& \mbox{名目GDP}\\ B_t & ：& 国債残高\\ \end{eqnarray}$

2. 証明

　国債発行額の対GDP比率 $\alpha$ を一定として、基礎的財政収支 $d_t^{PB}$ を決めるとすると、

となります。ここで、 $G_t$ はGDP、 $B_t$ は国債残高、 $r_t$ は国債金利です。

　GDP成長率を $g_t$ とすると、 $t$ +1時点における基礎的財政収支 $d_{t+1}^{PB}$ は、次式となります。

　基礎的財政収支の赤字が小さくならないように（財政支出ができるように）、金利 $r_{t+1}$ を制御することを考えます。このとき、金利 $r_{t+1}$ は、次の条件式を満たさなければなりません。

　等号が成り立つとき、これまでの基礎的財政収支の赤字幅は同額となります。金利がこれよりも小さいときには、国債発行額の対GDP比率 $\alpha$ を一定にしたままでも、基礎的財政収支の赤字を以前よりも大きくできます。つまり、財政支出を増やせます。

3. 具体例

　例えば、現在の国の予算をおおよその目安に、具体的に計算してみます。

GDP $G_t$ =500兆円、国債発行額対GDP比 $\alpha$ =4%として、国債発行額 $\alpha G_t$ =20兆円
国債残高 $B_t$ =1,000兆円、金利 $r_t$ = 1%として、利払い費 $r_tB_t$ = 10兆円

とすれば、基礎的財政収支 $d_t^{PB}$ =10兆円の赤字となります。

　このとき、GDPが翌年に成長率 $g_t$ =5% で成長すると、許容される金利 $r_{t+1}$ は1%から1.08%に若干増加します。

　金利は増えると言っても極僅かです。むしろ、5%成長しても、金利は1.08%とプラス0.08%以内に抑制しなければならないと言った方が適切でしょう。

　ほとんど金利上昇が許されないのは、GDP成長によって得られる国債発行額の余力は、新たに生まれるGDP増に1よりもずっと小さい定率 $\alpha$ を掛けていることと、債務残高が大きいことが原因です。

　国債残高 $B_t$ は毎年の国債発行額 $\alpha G_t$ よりも、通常は何倍も大きいので、金利が成長率の数分の一に抑制しなければなりません。

　つまり、経済成長しても、金利をそれに伴って増やすことができず、金融抑圧することが必要となります。

　金融抑圧できない場合には、基礎的財政収支の赤字を削減するか、もしくは、国債発行額の比率 $\alpha$ を大きくする必要があります。国債発行額の比率の引上げはドーマーの定理の条件を破ることになり、国債残高の対GDP比が発散する恐れがあります。

4. 成長が生み出す国債発行の余力

4.1 国債残高の余力

　成長率 $g$ が大きくなれば、国債残高 $B_t$ の対GDP比率の収束値 $\lim\frac{B_t}{G_t} = \frac{\alpha}{g}$ が小さくなります。逆に収束値を一定にするのならば、 $g$ =1%から5%と成長率が5倍となる例では $\alpha$ を5倍にしても、同じ収束値になり、 $\alpha$ に余力はできます。

　しかしながら、 $g$ =1%、 $\alpha$ =4%のときの国債残高の収束値は400%で既に大きな債務残高です。 $g$ =5%で $\alpha$ =20%となりますが、成長率が1%に戻ったとき国債発行額を1/5に抑制できなければ、収束値が2000%、GDP500兆円であれば1京円と巨額になります。

　債務残高の目標を $\frac{B_t}{G_t}$ =100%とするなら、 $\alpha$ =1×0.05=5% で若干の増加です。しかし、許容金利が1.08%から1.10%にわずかに増えるだけです。

　債務残高の目標を $\frac{B_t}{G_t}$ =200%なら、 $\alpha$ =2×0.05 = 10%ですが、許容金利は1.19%に留まります。

　また、マーストリヒト基準の60%なら、 $\alpha$ =0.6×0.05=3%なので、現状の4%でも国債発行額は多過ぎます。

4.2 国債発行額の余力

　成長率 $g_t$ と金利 $r_{t+1}$ が同じとなったときに、基礎的財政収支の赤字が減らないように $\alpha$ を変更する場合について考えます。基礎的財政収支の差分の式で、 $\alpha$ を時間に対する変数として、 $\alpha_t$ とすると、

　 $\alpha_t$ =4%、 $r_t$ =1%、 $r_{t+1}$ =5%、 $g_t$ =5%、 $G_t$ =500兆円、 $B_t$ =1,000兆円とすると、

　つまり、国債発行額の対GDP比は164%とは、GDP500兆円ならば、その年の1年の国債発行額が820兆円になり、現実的な数値とは言えません。

　なぜ、このようなことが起こるかというと、成長によって新たに生み出される国債発行額の余力 $\alpha_{t+1} g_t G_t$ が、利払い費の増加 $\alpha_t g_t G_t + (r_{t+1}-r_{t})B_t$ を超えなければならないためです。

　 $\alpha$ を極端に大きくはできませんので、利払い費の増加分を成長による国債発行額の拡大で補うことは期待できません。

4. 最後に

　ドーマーの定理の条件を満たすように毎年の国債発行額の対GDP比率を一定にしたときの、成長率と金利・国債残高に関する制約式について解説しました。

　基本的に成長率が大きくなったからといっても、基礎的財政収支の赤字枠はほとんど増えません。

　このため、金利を低金利に抑制するか、金利が上がるのであれば、増加した利払い費に見合った分の基礎的財政収支の赤字削減を行う必要があります。

　これを行わない限り、ドーマーの定理の条件を満たすことはできません。

(2019/9/2)

2019-08-30

ドーマーの定理の証明（３）：収束時の基礎的財政収支と成長率・金利の関係

ドーマーの定理

f:id:toranosuke_blog:20190830200634j:plain:w400

　これまでの記事で、オリジナルのドーマーの定理と米原・荒の条件について証明しましたが、ドーマーの定理では、成長率がプラスであれば、金利の大小に依らず、国債残高の対GDP比は収束します。このとき、成長率と金利と基礎的財政収支の間には、一定の関係があります。

　今回は、この関係について解説したいと思います。

1. 収束時の基礎的財政収支と成長率・金利の関係

　オリジナルのドーマーの定理によれば、毎年の国債発行がGDPの一定割合で、GDPがプラス成長するならば、国債残高の対GDP比は一定の値に収束します。

　収束したときの基礎的財政収支について、次の命題が成立します。これは、収束時における基礎的財政収支（プライマリーバランス）が、金利と成長率の大小によって、どのようになるかを示すものです。

収束時の基礎的財政収支の成長率・金利の関係
　GDPがプラス成長のときに、毎年の国債発行がGDPの一定割合となるように基礎的財政収支を調整すれば、収束段階では次の状態となる。

　成長率＞金利ならば、基礎的財政収支は赤字
　成長率＝金利ならば、基礎的財政収支は均衡
　成長率＜金利ならば、基礎的財政収支は黒字

　成長率と金利が同じならば、収束するに従って、PB均衡するように予算編成しなければならないという意味です。また、成長率が金利より高ければPB赤字、成長率が金利より低ければPB黒字での予算編成となります。　

2. 証明

　オリジナルのドーマーの定理では、国債残高 $B_t$ 、GDP $G_t$ は次のように表されます。

　ここで、 $b_t$ は毎年の国債発行額、 $\alpha$ は国債発行額のGDPに対する比率、 $g$ はGDP成長率で正の値です。国債発行額 $b_t$ は、利払い $rB_t$ と基礎的財政収支の赤字 $d_t^{PB}$ に分離して書き表すこともできます。

　さて、 $t$ と $t+1$ における対GDP比の国債残高の差は、次のようになります。

　これは、 $t\rightarrow\infty$ で零に収束しますので、

　ここで、ドーマーの定理*1から得られる $\displaystyle \lim_{t\rightarrow\infty}\frac{B_t}{G_t}=\frac{\alpha}{g}$ を代入しています。

　従って、収束時には、

成長率 $g$ ＞金利 $r$ で、基礎的財政収支 $d_t^{PB}$ は赤字
成長率 $g$ ＝金利 $r$ で、基礎的財政収支 $d_t^{PB}$ はゼロ
成長率 $g$ ＜金利 $r$ で、基礎的財政収支 $d_t^{PB}$ は黒字

3. 米原・荒の定理に適用した場合

　この定理で得られた収束時点での基礎的財政収支の対GDP比を米原・荒の定理*2における基礎的財政収支の対GDP比率とする場合について考えます。

3.1 成長率＞金利の場合

　 $g$ ＞ $r$ のときに、基礎的財政収支の対GDP比率 $\beta$ を

として、次式の国債発行額 $b_t$ で毎年国債を発行するとします。

　このとき、対GDP比の国債残高 $\frac{B_t}{G_t}$ は、米原・荒の定理より、次式に収束します。

　なお、国債発行額の対GDP比 $\frac{b_t}{G_t}$ は $\alpha$ に収束します。

3.2 成長率＜金利の場合

　成長率 $g$ ＜金利 $r$ の場合、基礎的財政収支 $d_t^{PB}$ が $\alpha(1-\frac{r}{g})G_t$ であっても、対GDP比の国債残高は、発散します。

　これは、次式の対GDP比国債残高は、 $\alpha=g\frac{B_0}{G_0}$ の場合を除いて、 $+\infty$ あるいは $-\infty$ に発散するためです。

　但し、例外的に $\frac{B_0}{G_0}=\frac{\alpha}{g}$ の場合、 $\frac{B_0}{G_0}$ に収束します。

　ドーマーの定理との違いがでるのは、ドーマー定理の場合には、国債発行額の対GDPの $\alpha$ は一定であるのに対して、米原・荒の定理では、 $\beta$ が一定で、 $\alpha$ は一定ではないからです。

3.3 成長率＝金利の場合

　成長率 $g$ ＝金利 $r$ のとき、 $\beta$ はゼロとなり、基礎的財政収支はゼロです。

　また、対GDP比国債残高の収束値は、 $\frac{B_0}{G_0}$ となります。この場合も、 $\alpha$ を一定としたときの収束値 $\frac{\alpha}{g}$ とは異なる値に収束します。

4. 具体例

　例えば、成長率 $g$ =2%、 $r$ =1%であれば、収束時の国債発行額の対GDP比率 $\alpha$ =6%がなるように、基礎的財政収支が対GDP比 $\beta=\alpha(1-\frac{r}{g})$ =3%の赤字とすれば、毎年の対GDP比の国債発行額は6%、対GDP比の国債残高は $\frac{\alpha}{g}$ =300%に収束し、安定的に推移します。

　なお、収束時の国債発行額6%の内訳は、3%は利払い費、3%がPB赤字分となります。

　仮に、金融抑圧によって金利 $r$ =0%にすることができれば、基礎的財政収支6%の赤字を毎年出せることになります。このとき、基礎的財政収支が赤字のままでも、国債残高は300%で安定的に推移します。

5. 最後に

　ドーマーの定理における収束時の基礎的財政収支と成長率・金利の関係について証明しました。今回、証明した命題は、次の通りです。

収束時の基礎的財政収支と成長率・金利の関係
　GDPがプラス成長のときに、毎年の国債発行がGDPの一定割合となるように基礎的財政収支を調整すれば、収束段階では次の状態となる。

　成長率＞金利ならば、基礎的財政収支は赤字
　成長率＝金利ならば、基礎的財政収支は均衡
　成長率＜金利ならば、基礎的財政収支は黒字

(2019/8/30)

*1:ドーマーの定理の証明（１）：元祖ドーマーの定理 - ゲゼルマネー経済学入門

*2:ドーマーの定理の証明（２）：金利と成長率に関する米原・荒の条件 - ゲゼルマネー経済学入門

2019-08-28

ドーマーの定理の証明（２）：金利と成長率に関する米原・荒の条件

ドーマーの定理利子率

f:id:toranosuke_blog:20190830212337j:plain:w300

　前回は、オリジナルのドーマーの定理について証明しました。

　今回は、金利と成長率に関連する条件である日本版ドーマーの定理の証明について書きます。日本版ドーマーの定理は、米原淳七郎氏、荒憲治郎氏がそれぞれ独立に条件を導いたそうです。米原・荒の条件と言った方がよいのかもしれません*1。

　今回は、この米原・荒の条件について証明します。

1. 金利と成長率に関する米原・荒の条件

　オリジナルのドーマーの定理は、「国債発行がGDPの一定割合ならば、財政破綻しない」ですが、ここには、隠れた条件「経済成長がプラス成長すること」があります。この隠れた条件について、成長率に加えて、金利も考慮したものが、日本版ドーマーの定理、米原・荒の条件です。

　日本版ドーマーの定理は、次のように言われます。

日本版ドーマーの定理
GDP成長率が国債金利を上回れば、財政破綻は生じない。
（GDP・金利はともに名目値）

　ここでの「財政破綻は生じない」の意味は、「国債残高の対GDP比は発散しない」という意味です。

　前回の記事に倣って、言い換えると、

米原・荒による金利と成長率に関する条件
GDP成長率が国債金利を上回れば、国債残高の対GDP比は一定の値に収束する。

となります。

　この定義では、今度は「国債発行がGDPの一定割合であること」に相当する条件が隠れてしまっていますが、それは後ほど説明します。

2. 定理の証明

2.1 国債金利と基礎的財政収支

　ある年の国債残高を $B_t$ 、国債金利を $r$ ( $r$ > 0) とします。すると、その年の利払いは $rB_t$ となります。その年に必要な国債発行額 $b_t$ は、次のようになります。

　ここで、 $d^{PB}_t$ は、基礎的財政収支（プライマリーバランス）の赤字のことで、利払いを除いた財政赤字額です*2。

2.2 対GDP比の国債残高

　このとき、新規国債発行後の国債残高 $B_{t+1}$ は、次の通りです。

　従って、

2.3 一定の経済成長を仮定

　　GDP成長率を $g$ とすると、

　第1項は $r$ < $g$ 、つまり、国債金利が成長率より小さければ、 $t$ → $\infty$ にてゼロに収束します。しかし、第2項の収束性は $d^{PB}_i$ が不明ですので、判定できません。

2.4 対GDP比の基礎的経済収支は一定を仮定

　このため、基礎的財政収支 $d^{PB}_i$ は、GDP $G_i$ に対して一定割合と仮定します。

　この仮定がドーマーの定理の「国債発行がGDPに対して一定割合であること」に対応します。

　従って、 $r$ < $g$ 、あるいは、 $\frac{B_0}{G_0} = \frac{\beta}{g-r}$ の場合に $\frac{\beta}{g-r}$ に収束します。

また、 $r$ = $g$ 、且つ、 $\beta$ =0 で、 $\frac{B_0}{G_0}$ に収束します。それ以外の場合は、発散します。

2.5 金利と経済成長率は一定でなくてもよい

　ドーマーの定理の場合と同様に金利と経済成長率は一定でなくて構いません。次の条件が成り立っていれば、収束します。

　この条件が満たされれば、 $\frac{1+r_t}{1+g_t}$ < 1 となり、オリジナルのドーマーの定理と同様に収束は保証されます。

　この場合、 $g_t$ < 0、つまり、マイナス成長であっても、収束します。しかし、金利もマイナス金利であることが必要なので、通常はありません*3。

3. プライマリーバランスの均衡

3.1 PB均衡は、十分条件

　プライマリーバランス(PB)の均衡が保たれることが、財政破綻しないための条件かのように言われていますが、必ずしもそうではありません。

　プライマリーバランスの均衡とは、つまり、基礎的財政収支 $d^{PB}_t$ = 0 ということです。この場合、式の第2項はゼロになり、 $r$ < $g$ のもと、対GDP比の国債残高はゼロに収束していきます。つまり、借金はなくなります。しかし、これは十分条件であって、必要条件ではありません。

3.2 PB赤字でも、財政破綻しない

　 $d^{PB}_t$ > 0 で基礎的財政収支が赤字であれば、 $\frac{\beta}{g-r}$ に国債残高のGDP比が収束しますので、ドーマーの定理の意味での財政破綻は生じません。

　しかし、前回も述べたようにドーマーの定理での財政破綻は、単に対GDP比の国債残高が発散しないことを意味するだけで、実際に財政が破綻がしないということを保証するわけではありません。

　詳しくは、次回の記事で説明します。

3.3 PB黒字であれば、債権を蓄積

　 $d^{PB}_t$ < 0 の場合も同様に、 $\frac{\beta}{g-r}$ に収束します。但し、この場合は、 $\beta$ がマイナスですので、マイナス債務、つまり、GDP比で一定の債権が蓄積されるということになります。

　プライマリーバランスの黒字が利払いよりも大きくなっていれば、財政黒字ですので、国債残高の絶対額が減少します。

　また、当初は、利払いの方がプライマリーバランスの黒字よりも大きく財政赤字であったとしても、対GDP比で一定の割合でプライマリーバランスの黒字を継続すれば、利払いによる赤字とプライマリーバランスの黒字が均衡する、つまり、財政収支がゼロとなるポイントに到達します。

　これを超えると、プライマリーバランスの黒字は財政黒字となり、国債残高の絶対額が減少し、遂には国債残高はゼロになります。

　その後の財政黒字を積み上げるのであれば、金利がある債権を国が蓄積することになりますが、これは、現実問題としては発生しないでしょう。

4. 金利と成長率

4.1 金利 < 成長率とはならない

　GDP成長率 $g$ が国債金利 $r$ を上回っていれば、対GDP比の国債残高の収束が期待されますが、実際はどのようになっているでしょうか？

　下図は、日本と米国における国債金利とGDP成長率の推移を示しています。

f:id:toranosuke_blog:20190828010331p:plain

日本における国債金利とGDP成長率の推移 （文献*4より引用）

f:id:toranosuke_blog:20190828010957g:plain

f:id:toranosuke_blog:20190828095342g:plain

米国における国債金利とGDP成長率の推移（文献*5より引用）

1980年以前はr＜g、1980年～2002年頃はr＞g、2003年以降はリーマンショック時を除きr＜gで推移している。2000年代は政府債務を増やしながらの経済成長であるので、対GDP比の政府債務は増加している。

　日本は、1981年以降、バブル期の一部と、2013年以降にしか、GDP成長率が金利を超えていません。平均的には $r$ > $g$ であり、対GDP比の国債残高は発散し、財政破綻します。

　米国のデータは10年国債の金利で、短期国債や超長期国債を含めた加重平均での国債金利ではありませんが、多少のずれを考慮しても、安定的に $r$ < $g$ の破綻しない条件を満たしているとは言い難いです。

　日米の金利・成長率のグラフを見る限りでは、金利が経済成長率より小さくなるとは言えません。

4.2 金融抑圧

　普通の金融政策を行っている場合には、 $r$ < $g$ になるとは限りませんが、政策的に金利を低くすること、つまり、金融抑圧によって、 $r$ < $g$ を実現することが過去に実施されています。

　例えば、第2次世界大戦直後の英国が金融抑圧によって債務縮小を実現した例と言われます*6。図は、英国における利回りと名目成長率の推移を表しています*7。終戦後から1960年頃まで、GDP成長率が利回りを上回り、 $r$ < $g$ の状況を実現していることが分かります。

f:id:toranosuke_blog:20190828015525p:plain:w500

英国における利回りと名目GDP成長率（文献*8より引用）

f:id:toranosuke_blog:20190828094758j:plain

英国における政府債務比率・長期金利・物価上昇率の推移（文献*5より引用）

　戦後、対GDP比250%以上の政府債務を背負った英国は国債金利を規制によって5%以下に固定しました。この金融抑圧や戦後の経済成長なども相まって、対GDP比の政府債務を大幅に縮小することができました。

4.3 日本の異次元緩和政策

　日本は日銀の異次元緩和によって、低金利誘導を行っているため、低金利が継続しています。一方、名目GDPは2011年以降増加していますので、プラス成長です。従って、 $r$ < $g$ が実現できている状況にあります。

　しかし、これは日銀の巨額の国債購入で実現しているために、今後、銀行危機や日銀債務超過などの副作用が表面化することが懸念されています。

　基本的には、経済成長率が国債金利を安定的に超えることは期待できないでしょう。

　従って、対GDP比の政府債務を一定程度に納めるのであれば、米原・荒の条件を用いて基礎的財政収支を基準にするのではなく、EUのマーストリヒト基準のように、オリジナルのドーマーの定理に基づいて、財政収支を基準に考えた方が良いのかもしれません。

5. 最後に

　日本版ドーマーの定理、つまり、米原・荒による金利と成長率に関する条件について証明しました。証明のために必要であった条件を付け加えると、今回、証明した命題は、次の通りです。

米原・荒による金利と成長率に関する条件
毎年の基礎的財政収支がGDPの一定割合で、GDP成長率が国債金利を上回れば、国債残高の対GDP比は一定の値に収束する。

(2019/8/28)

*1:畑農鋭矢, 「ドーマー条件～第３の謎「出生の秘密」」(2011).

*2:「基礎的財政収支（プライマリー・バランス）とは、税収・税外収入と、国債費（国債の元本返済や利子の支払いにあてられる費用）を除く歳出との収支のこと」（財務省ホームページ）

*3:しかし、現在では、日本やドイツ、スイスなどの国債で、マイナス金利となっています。特にドイツ国債は30年債という超長期国債でも、マイナス0.11%の金利を付けています。
・Quick Mony World, 「欧州、沈む金利　ベルギーもマイナス、ドイツは中銀預金金利を下回る」, 2019.7.5.
・豊島逸夫, 「ドイツ「金利沈没」の衝撃」, 日本経済新聞, 2019.8.22.
・Bloomberg, 「国債全年限でマイナス金利化の足音、世界的なプラス利回り争奪激化で」, 2019.8.23.

*4:小黒一正, 「中長期試算の前提を考える－「金利・成長率」論争の再燃か－」(2018).

*5:Ed Yardeni, "The Bond Yield & GDP (excerpt)" (2013).

*6:池田信夫, 「日本は「金融抑圧」で政府債務を踏み倒せるか」, アゴラ, 2019.3.13.

*7:利回りは株式利回りのため必ずしも国債金利を表すわけではありませんが、ある程度相関はあると考えられます。

*8:BOND VIGILANTES, "Long-dated UK government bond yields are closely correlated to nominal GDP growth"

2019-08-23

ドーマーの定理の証明（１）：元祖ドーマーの定理

ドーマーの定理

f:id:toranosuke_blog:20190828085532j:plain:w280

　「インフレにならない限り、国債発行しても構わない」という反緊縮派の主張がありますが、MMTにおける財政スペースの増加量とドーマーの定理において許容される債務増加量が、ある条件下では、同じになり、対GDP比の国債残高は発散しないと推測しています。

　そこで、まずはドーマーの定理について勉強しようと思いましたが、面白いことに、ドーマーの定理については二つあるとのことです。金利と成長率に関するドーマーの定理は日本オリジナルのものらしいです。

　今回の記事では、本家のドーマーの定理とその証明について、書きたいと思います。

1. ドーマーの定理

　金融情報サイトiFinance *1では、ドーマーの定理を次のように説明しています。

ドーマーの定理は、「ドーマーの条件」とも呼ばれ、1940年代にロシア系アメリカ人の経済学者エブセイ・ドーマー（Evsey David Domar：1914/4/16－1997/4/1）によって提唱された、財政赤字の維持可能性に関する定理（条件）のことをいいます。これは、元々は、① 毎年の国債発行がGDPの一定割合に留まるならば、国債残高の対GDP比は一定の値に収束して財政破綻は生じないという概念でしたが、現在、日本においては、② 名目GDP成長率が名目公債利子率を上回れば、財政赤字は維持可能であるという概念になっています。
（①、②、太字は筆者が追加）

　本家のドーマーの定理は、①の「毎年の国債発行がGDPの一定割合に留まるならば、国債残高の対GDP比は一定の値に収束して財政破綻は生じない」の方です。②が日本版ドーマーの定理です。

　二つあるドーマーの定理については、明治大学の畑農鋭矢教授のブログに詳しく解説されています（付録参照）。

2. 定理の証明

　理解を深めるために、ドーマーの定理について証明をしました。

　定理の証明について調べてもすぐには見つかりませんでした。ドーマーのオリジナルの論文*2に書いてあるのかもしれませんが、特に難しそうでもないので、独自に証明しました。

2.1 証明する命題

　ドーマーの定理の「財政破綻しない」という命題は、そもそも誤りです。「一定割合」に条件が付けば、必ずしも誤りとは言えないと思いますが、その条件は示されていません。

　ドーマーの定理で財政破綻しないのは、国債残高に対する利払いが小さいという暗黙の仮定があるためと思われます。たとえ、国債残高が一定値に収束したとしても、その国債残高が大きくなり、利払いが大きくなれば、国家予算を組むことはできなくなるでしょう。この点に着目したのが、日本版ドーマーの定理です。

　従って、ここで証明するのは、「一定の値に収束する」という次の命題です。

ドーマーの定理
毎年の国債発行がGDPの一定割合に留まるならば、国債残高の対GDP比は一定の値に収束する。

2.2 対GDP比の国債残高

　毎年、GDP $G_t$ に対して $\alpha$ の比率で国債を発行するとき、毎年の国債発行額 $b_t$ は次式となります。

　新規国債発行後の国債残高 $B_{t+1}$ は、次式です。

　従って、

　両辺を $G_t$ で割ると、

　この条件だけでは、収束しませんね。 $G_t$ の値が不明だからです。

2.3 一定の経済成長を仮定

　GDPは、成長率 $g$ （ $g>0$ ）で毎年成長すると仮定しましょう。すると、

　右辺第1項は、 $t\rightarrow \infty$ でゼロに収束します。第2項は、等比数列の和で、これも収束します。 $t\rightarrow \infty$ での収束値は、次式となります。

　なお、 $g\le0$ であれば、対GDP比の国債残高は発散します。

2.4 経済成長は一定でなくてもよい

　前節では、GDP成長率 $g$ は一定としましたが、一定でなくとも、 $g_t>0$ であれば、収束します。

　最小の成長率を $g_\min$ とすると、最小の成長率のときの対GDP比の国債残高は $\frac{\alpha}{g_\min}$ に収束しますが、国債残高比の式の第2項の級数の各項は、 $g_\min$ の場合の各項よりも小さくなるので、最小成長率の収束値よりも小さな値に収束します（級数の収束に関する比較判定法）。

2.5 財政破綻せずとも、経済破綻する

　ドーマーの定理では、 $\alpha$ がいくら大きな値であっても、発散することはなく、収束します。

　例えば、成長率が1%で、 $\alpha$ =1（対GDP比100%の国債発行）であったとしても、対GDP比の国債残高は収束します。しかし、収束値は、対GDP比が100（10,000%）です。500兆円のGDPなら5京円の国債残高です。発行した国債を中央銀行が引き受ければ、国債消化はでき、財政は破綻しないかもしれません。しかし、国債残高が5京円に到達する前にハイパーインフレなどが発生し、経済は破綻するでしょう。

　つまり、ドーマーの定理の「財政破綻しない」という命題は、そもそも誤りなのです。単に対GDP比の国債残高が発散しないと言っているに過ぎず、財政が破綻しないことを保証するわけではありません。

2.7 毎年の国債発行額

　毎年の赤字発行額の対GDP比 $\alpha$ を $g\gamma$ にすれば、国債残高の対GDP比は、 $\gamma$ に収束します。

　つまり、債務残高の対GDP比の目標値が $\gamma$ ならば、毎年の国債発行額 $b_t$ は次式の発行額にすればよいです。

　例えば、目標とする国債残高の対GDP比が $\gamma$ =100%で、GDP成長率 $g$ =2%、GDP 500兆円ならば、発行できる国債発行額は10兆円となります。

3. 収束値の例

3.1 計算表

　具体的に数字を入れてみます。

　GDPが500兆円のとき、国債発行額30兆円とすれば、 $\alpha$ =6%ですが、その比率で国債を毎年発行するとします。そして、GDP成長率が $g$ =2%なら、対GDP比の国債残高は、次の値に収束します。

　この場合、対GDP比300%の国債残高に収束します。

　 $\alpha$ と $g$ を変更して、表にしました。

	$\alpha$ =1% (5兆円)	$\alpha$ =2% (10兆円)	$\alpha$ =4% (20兆円)	$\alpha$ =6% (30兆円)	$\alpha$ =8% (40兆円)	$\alpha$ =10% (50兆円)
g=0.5%	2.0	4.0	8.0	12.0	16.0	20.0
g=1%	1.0	2.0	4.0	6.0	8.0	10.0
g=2%	0.5	1.0	2.0	3.0	4.0	5.0
g=3%	0.33	0.66	1.33	2.0	2.66	3.33
g=4%	0.25	0.50	1.0	1.5	2.0	2.5
g=5%	0.20	0.40	0.8	1.2	1.6	2.0

括弧内は、GDPが500兆円のときの国債発行額。

3.2 一般会計の例

　また、国の一般会計の数字を用いて計算すると、次のようになります*3。

2018年度
- $\alpha=\frac{\mbox{公債費35.4兆円-債務償還費14.3兆円}}{\mbox{名目GDP 552.5兆円}}$ =3.8%
- 名目GDP成長率 $g=0.9$ %
- 対GDP比国債残高の収束値：424%
2019年度
- $\alpha=\frac{\mbox{公債費32.7兆円-債務償還費14.6兆円}}{\mbox{名目GDP 566.1兆円}}$ =3.2%
- 名目GDP成長率 $g=2.4$ %
- 対GDP比国債残高の収束値：133%

　2018年度と2019年度で収束値が424%と133%と大幅に違いますが、経済成長率が2倍以上異なることが大きく影響しています。

3.3 EUのマーストリヒト基準

　EUではマーストリヒト基準によって、財政規律を求めています。この基準の中には、次の二つの制約があります。

単年度の新規国債発行額は、対GDP比で3%以下（ $\alpha\le$ 3%）。
債務残高は、対GDP比で60%以下。

　ドーマーの定理より、債務比率60%以下となるために必要な成長率 $g$ は、

　つまり、新規国債発行額が対GDP比3%であっても、経済成長率 $g$ = 5%以上であれば、債務比率60%以下を満たすことができます。

　しかし、経済成長率5%は必ずしも実現できるものではなく、達成可能な経済成長率を2%とすれば、

　日本のGDPを566.1兆円(2019)とすれば、僅か6.8兆円の新規国債発行しか許されません。現在、（償還分を除いて）18.4兆円の新規国債を発行している日本からすれば、厳しい基準となります。

4. 最後に

　ドーマーの定理を証明しました。証明のために必要であった条件を付け加えると、今回証明したドーマーの定理は、次の命題です。

ドーマーの定理
毎年の国債発行がGDPの一定割合で、GDPがプラス成長するならば、国債残高の対GDP比は一定の値に収束する。

　次回の記事では、プライマリーバランスに関係する日本版ドーマーの定理について、証明したいと思います。

(2019/8/23)

(追記：2019/8/24)　ドーマーの定理の証明がありました*4。漸化式ではなく、連続関数で証明していますが、基本的に同じ考え方で、収束値も同一です。

(追記：2019/9/1)　毎年の国債発行額の対GDP比率 $\alpha_t$ は一定でなくても、発散しません。これは、 $\alpha_t$ の最大値を $\alpha_\max$ としたときに、 $t\rightarrow\infty$ の極限の国債残高の対GDP比の値は、 $\frac{\alpha_\max}{g_\min}$ よりも小さくなるからです（但し、収束条件を満たさないために、値が安定するとは限りません）。

　従って、最も条件を緩めた場合のドーマーの定理の命題は、次のようになります。

（最も条件が緩い）ドーマーの定理
毎年の国債発行の対GDP比率によらず、GDPがプラス成長するならば、国債残高の対GDP比は発散しない。
（但し、国債発行の対GDP比率が無限大である場合、及び、GDP成長率が無限小のプラス成長率である場合は除く）

　要するに、プラス成長だけが、対GDP比の国債残高が発散しない条件です。これは、ドーマーの定理の意味では「財政破綻しない」ことになりますが、政府債務が非常に大きくなれば、実際には国の経済は破綻しますので、破綻条件としてはほとんど意味をなしていません。

付録：畑野教授のブログ

　畑野教授のブログ「もう一度よく考え直してみてよ」に、ドーマー条件に関連する記事が投稿されています。それらの記事をリストアップしました。

　一連の記事は面白いです。特に、本家ドーマーの定理と日本版ドーマーの定理の謎についての記事は、特筆すべきものがあります。

　古いブログ記事でリンクがメンテされておらず、記事を追いかけるのが少々面倒です。また、「米原・荒条件（ドーマー条件）の導出」のリンク先のPDFにアクセスできない点は、ちょっと残念でした。

ドーマー条件～３つの謎（2011.6.6）
ドーマー条件～第1の謎「二つのドーマー定理」(2011.6.13）
ドーマー条件～第２の謎「ルーツ探索」（2011.6.25）
ドーマー条件～第３の謎「出生の秘密」（2011.7.15）
ドーマー条件～３つの誤解（2011.9.15）
米原・荒条件（ドーマー条件）の導出（2011.9.22）
ボーン条件とドーマー条件（2011.12.9） +ボーン条件の補足（2011.12.11）
「ボーン条件の補足」の補足（2011.12.20）

*1:金融情報サイトiFinance, 「ドーマーの定理」.

*2:Evsey D. Domar, "The Burden of the Debt and the National Income," American Economic Review, 34(4), pp.798-827 (1944) . （日本語訳：E.D.ドーマー［宇野健吾訳］『経済成長の理論』東洋経済新報社，第２章 (1959)．(amazon)）

*3:公債費・債務償還費は、財務省「債務管理リポート2019」のp166, p168参照。
名目GDP、名目GDP成長率は平成31年度予算のポイントのp4参照。

*4:石田昌夫, 「財政赤字問題の再検討」,産業経済研究所紀要, 第15号, 2005.3.

1. 節税対策としての永久国債

2. 相続税の課税対象から除外

3. 物納を可能にする

4. 物納額に上限を付ける

4.1 物納上限値

国債保有比率 y=1/3、税率 z=1/2 の場合

4.2 最適な国債保有比率

y=z=1/2の場合

4.3 物納上限を言葉で表す

5. 増税

5.1 税率を50%から75%にあげた場合

5.2 納税後も「資産」が減らない国債保有比率

6. 最後に

1. 貨幣数量説に基づく国債残高の収束性

2. 証明

2.1 フィッシャーの交換方程式

2.2 国債発行額

2.3 国債発行額の対GDP比

2.4 貨幣流通速度に対する収束性

貨幣流通速度が一定の場合、国債残高は収束する

貨幣流通速度が上昇すれば、債務残高はゼロに収束する

貨幣流通速度が下降すれば、債務残高は発散する

3. 具体例

3.1 簡単な例

貨幣流通速度の変化率 =0% の場合

貨幣流通速度の変化率 =-1.5% の場合

3.2 2018年の日本のデータを用いた試算

4. 貨幣流通速度低下時に債務が発散しない条件

5. 貨幣流通速度と成長率の関係

6. 貨幣流通速度を上昇させるための税制

6.1 眠った現預金は貨幣流通速度を低下させる

6.2 税金でお金の流れを誘導する

7. 最後に

関連記事

付録：民間貸出による市中銀行の貨幣供給

1. インフレ率ゼロのときの成長率と国債発行額の関係

2. 証明

2.1 貨幣数量説

2.2 貨幣量の増加

2.3 GDPの増加

2.4 GDPと貨幣量の関係

2.5 国債発行額と貨幣の増加量

2.6 ドーマーの定理の適用

3. 具体例

4. MMTとの関係

5. 最後に

関連記事

1. 成長率と金利・国債残高の制約関係

2. 証明

3. 具体例

4. 成長が生み出す国債発行の余力

4.1 国債残高の余力

4.2 国債発行額の余力

4. 最後に

関連記事

1. 収束時の基礎的財政収支と成長率・金利の関係

2. 証明

3. 米原・荒の定理に適用した場合

3.1 成長率＞金利の場合

3.2 成長率＜金利の場合

3.3 成長率＝金利の場合

4. 具体例

5. 最後に

関連記事

1. 金利と成長率に関する米原・荒の条件

2. 定理の証明

2.1 国債金利と基礎的財政収支

2.2 対GDP比の国債残高

2.3 一定の経済成長を仮定

2.4 対GDP比の基礎的経済収支は一定を仮定

2.5 金利と経済成長率は一定でなくてもよい

3. プライマリーバランスの均衡

3.1 PB均衡は、十分条件

3.2 PB赤字でも、財政破綻しない

3.3 PB黒字であれば、債権を蓄積

4. 金利と成長率

4.1 金利 < 成長率とはならない

4.2 金融抑圧

4.3 日本の異次元緩和政策

5. 最後に

貨幣流通速度の変化率 $v_t$ =0% の場合

貨幣流通速度の変化率 $v_t$ =-1.5% の場合